Usa R!

Una introducción a la programación

José Antonio López Gómez

¿Qué es “programar”?

Programar es el proceso de crear un conjunto de instrucciones para decirle a la computadora cómo realizar una tarea.

¿Cómo programar?

La tarea de “programar” no se centra exclusivamente en escribir código, si no que conlleva una serie de pasos previos antes de “codificar” las instrucciones.

Descomponer un problema complejo en partes más pequeñas.
Reconocimiento de patrones repetitivos.
Resolución de los problemas paso a paso.
Escribir el código.

¿Qué es un “lenguaje de programación”?

Un lenguaje de programación es un lenguaje formal (es decir, un lenguaje con reglas gramaticales bien definidas) que proporciona al programador la capacidad y habilidad de escribir instrucciones o secuencias de órdenes para controlar el comportamiento de un sistema informático.

¿El entorno de R?

R es un conjunto integrado de software para la manipulación, cálculo y visualización de datos. Entre otras cosas tiene:

Tratamiento y almacenamiento de datos eficaz.
Conjunto de operadores para el calculo sobre matrices.
Conjunto integrado de herramientas para el análisis y visualización de datos.
Un simple y efectivo lenguaje de programación.
Ampliamente utilizado en investigación cientifica.

¿Qué es un “Programa”?

Un programa informático es una secuencia de instrucciones basadas en un lenguaje de programación que el ordenador interpreta para resolver un problema.

¿Cuales son los elementos básicos de un programa?

Instrucciones: conjunto de ordenes que indican al ordenador como realizar una tarea específica (asignar un valor a una variable, ejecutar un bucle que itera sobre una lista de datos).

Funciones: conjunto de instrucciones que permiten realizar una tarea específica (ANOVA, plot de datos, etc..). Se pueden imaginar como una máquina que toma ciertos datos, realiza una operación y devuelve un resultado.

¿Cuales son los elementos básicos de un programa?

Datos: pueden ser números, texto, imagénes, etc.. . En resumen cualquier tipo de información que el programa manipule. En general, son la razon de ser de muchas aplicaciones.

Operadores: son las herramientas que permiten realizar operaciones sobre los datos (sumar, multiplicar, comparar, asignar, etc..).

Variables: actuan como contenedores de información permitiendo que un programa conserve información y realice operaciones sobre esta información, en cierto modo se puede decir que son la “memoria” del programa.

“¡Hola Mundo!”

El programa “¡Hola Mundo!” suele ser el primer ejercicio típico en la introducción del estudio de un lenguaje de programación.

saludo <- "¡Hola Mundo!"

saludo

[1] "¡Hola Mundo!"

Usando funciones

- head()

Para ilustrar el uso de la función head() utilizaremos el dataset iris que viene con la instalación de R-Base.

df <- iris

head(df)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

Usando funciones

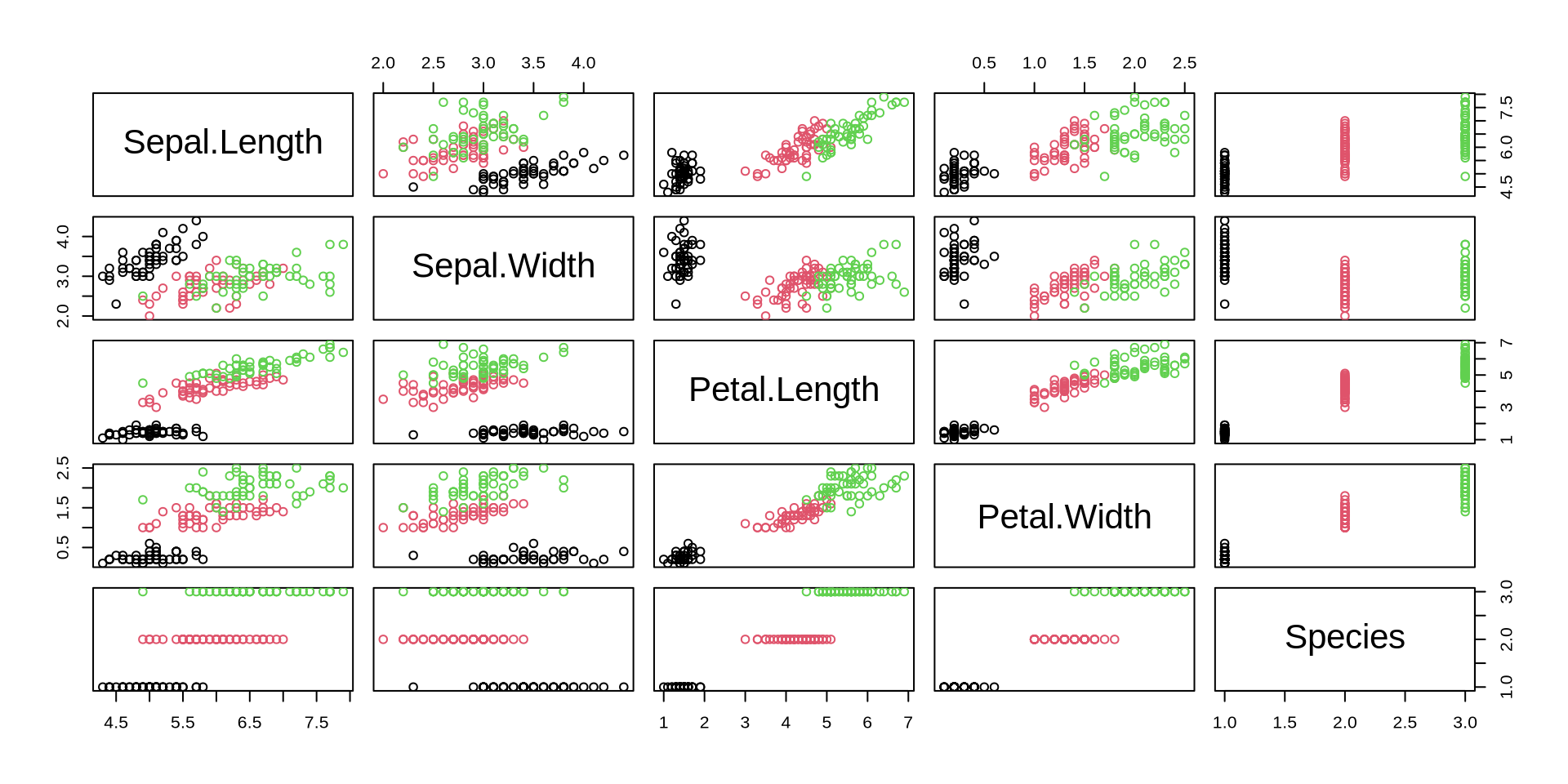
- pairs()

Para ilustrar el uso de la función pairs() utilizaremos el dataset iris que viene con la instalación de R-Base.

df <- iris

pairs(df, col = df$Species)

Estructuras de control de flujo

Se llaman estructuras de control de flujo a las instrucciones que permiten controlar las acciones de un algoritmo o programa. Estas son de gran utilidad para determinar la lógica y el orden en que ocurren las operaciones.

if, else: if(“si”) es usado cuando deseamos que una operación se ejecute únicamente cuando una condición se cumple. else(“de otro modo”) es usado para indicar que hacer en cado de que la condición de un if no se cumpla.
for: nos permite ejecutar un bucle, realizando una misma operación para cada elemento de un conjunto de datos.

if, else

variable_1 <- 5

if (variable_1 >10) {
    print('la variable_1 es mayor que 10')
} else {
    print('la variable_1 NO es mayor que 10 ')
}

[1] "la variable_1 NO es mayor que 10 "

for

estaciones <- c('primavera', 'verano', 'otoño', 'invierno')

for(estacion in estaciones){
    print(toupper(estacion))
}

[1] "PRIMAVERA"
[1] "VERANO"
[1] "OTOÑO"
[1] "INVIERNO"

Variables

Las variables actuan como contenedores de información (“memoria”) del programa. La estructura de esa información es muy heterogenea, podemos tener información simple(el número 5, el texto “¡Hola Mundo!”, etc..) o mucho más compleja (matriz de RNA-seq, con miles de filas y columnas).

En base al tipo de información que contienen las variables las podemos clasificar en simples o complejas.

Variables simples

Tipo de dato	Descripción	Definición
Numeric	Números decimales	numero <- 1.0
Integer	Números enteros	entero <- 1
Character	Cadenas de texto	texto <- “un texto”
Complex	Números complejos	complejo <- 3 + 2i
Logical	TRUE o FALSE	5 < 6; 5 == 5
Factor	Es una variable de tipo categórica

Variables complejas

La estructura de la información contenida en estas variables es más compleja. Además estas variables tienen métodos y atributos que facilitan acceder a la información que contienen.

Vectores: Los vectores almacena una secuencia de valores simples todos del mismo tipo.
Listas: A diferencia de los vectores las listas es una colección de elementos que pueden ser de diferente tipo.
Matrices:Una matriz es una estructura bidimensional que almacena números.
Data Frames: Un Data Frame es una estructura bidimensional que puede almacenar tipos de datos mixtos.

Vectores

La forma más habitual de crear un vector es usando la función c()

vector_numeros <- c(2, 4, 6, 8)
print(vector_numeros)

[1] 2 4 6 8

seq_numeros <- 10:20
print(seq_numeros)

 [1] 10 11 12 13 14 15 16 17 18 19 20

comb_vect <- c(vector_numeros, seq_numeros)
print(comb_vect)

 [1]  2  4  6  8 10 11 12 13 14 15 16 17 18 19 20

Aritmética de Vectores

Las operaciones aritméticas con vectores se realizan posición a posición.

vector_numeros <- seq(10, 50, by = 5)
print(vector_numeros)

[1] 10 15 20 25 30 35 40 45 50

print(vector_numeros + 1)

[1] 11 16 21 26 31 36 41 46 51

print(vector_numeros / 2)

[1]  5.0  7.5 10.0 12.5 15.0 17.5 20.0 22.5 25.0

Aritmetica de Vectores

Dos vectores

vector_numeros_1 <- c(1, 2, 3, 4)
vector_numeros_2 <- c(1, 1, 0, 0)
print(vector_numeros_1 - vector_numeros_2)

[1] 0 1 3 4

print(vector_numeros_1 * vector_numeros_2)

[1] 1 2 0 0

Aritmetica de Vectores

Vectores texto y números

letras <- c('A', 'B', 'C', 'D')
numeros <- c(1, 2, 3, 4)
print(paste0(letras, numeros))

[1] "A1" "B2" "C3" "D4"

print(paste0(numeros, letras))

[1] "1A" "2B" "3C" "4D"

Elementos vector

numeros <- 10:20
numeros

 [1] 10 11 12 13 14 15 16 17 18 19 20

numeros[4]

[1] 13

numeros[-4]

 [1] 10 11 12 14 15 16 17 18 19 20

numeros[c(4:8)]

[1] 13 14 15 16 17

numeros[-c(4:8)]

[1] 10 11 12 18 19 20

numeros[c(2, 10)]

[1] 11 19

Elementos vector

numeros <- 10:20
numeros

 [1] 10 11 12 13 14 15 16 17 18 19 20

numeros[-c(4:8)]

[1] 10 11 12 18 19 20

numeros <- numeros[-c(4:8)]
numeros

[1] 10 11 12 18 19 20

numeros <- c(numeros, c(1, 2, 3))
numeros

[1] 10 11 12 18 19 20  1  2  3

numeros <- numeros[order(numeros, decreasing = TRUE)]
numeros

[1] 20 19 18 12 11 10  3  2  1

Máscara lógica

numeros <- 10:20
numeros

 [1] 10 11 12 13 14 15 16 17 18 19 20

numeros < 15

 [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE

numeros[numeros < 15]

[1] 10 11 12 13 14

mascara_logica <- numeros == 10
mascara_logica

 [1]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

!mascara_logica

 [1] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

numeros[!mascara_logica]

 [1] 11 12 13 14 15 16 17 18 19 20

Conclusión

Para seleccionar subconjuntos de datos lo podemos realizar de dos formas:

Vector de índices

numeros <- runif(10, min = 1, max = 1000)
numeros

 [1] 890.54327 826.37310 251.42079 945.70646 598.31414  29.88844 310.83362
 [8] 455.57611 602.91052 300.44098

numeros[c(1, 5, 10)]

[1] 890.5433 598.3141 300.4410

Máscara lógica

numeros[numeros < 500]

[1] 251.42079  29.88844 310.83362 455.57611 300.44098

Data Frame

Un data frame es una estructura de datos bidimensional pudiendo almacenar datos mixtos(texto, números, etc ..). Un data frame es una lista de vectores (columnas) de la misma longitd.

df <- iris

dim(df)

[1] 150   5

head(df)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

summary(df)

  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
       Species  
 setosa    :50  
 versicolor:50  
 virginica :50

Structure of an Arbitrary R Object

La función str() muestra la estructura interna de un Objeto(variable compleja) de R.

df <- iris

str(df)

'data.frame':   150 obs. of  5 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

df$Sepal.Length

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

Seleccionar una columna

df$Sepal.Length

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

df[, c('Sepal.Length')]

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

df[, c(1)]

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

Seleccionar varias filas y columnas

df[1:10, c('Sepal.Length', 'Species')]

   Sepal.Length Species
1           5.1  setosa
2           4.9  setosa
3           4.7  setosa
4           4.6  setosa
5           5.0  setosa
6           5.4  setosa
7           4.6  setosa
8           5.0  setosa
9           4.4  setosa
10          4.9  setosa

df[c(30, 40, 100), c(5, 2, 4)]

       Species Sepal.Width Petal.Width
30      setosa         3.2         0.2
40      setosa         3.4         0.2
100 versicolor         2.8         1.3

Subset

df[df$Species == 'versicolor' & df$Sepal.Length > 6, ]

   Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
51          7.0         3.2          4.7         1.4 versicolor
52          6.4         3.2          4.5         1.5 versicolor
53          6.9         3.1          4.9         1.5 versicolor
55          6.5         2.8          4.6         1.5 versicolor
57          6.3         3.3          4.7         1.6 versicolor
59          6.6         2.9          4.6         1.3 versicolor
64          6.1         2.9          4.7         1.4 versicolor
66          6.7         3.1          4.4         1.4 versicolor
69          6.2         2.2          4.5         1.5 versicolor
72          6.1         2.8          4.0         1.3 versicolor
73          6.3         2.5          4.9         1.5 versicolor
74          6.1         2.8          4.7         1.2 versicolor
75          6.4         2.9          4.3         1.3 versicolor
76          6.6         3.0          4.4         1.4 versicolor
77          6.8         2.8          4.8         1.4 versicolor
78          6.7         3.0          5.0         1.7 versicolor
87          6.7         3.1          4.7         1.5 versicolor
88          6.3         2.3          4.4         1.3 versicolor
92          6.1         3.0          4.6         1.4 versicolor
98          6.2         2.9          4.3         1.3 versicolor

Columnas

df$Sepal.Ratio <- df$Sepal.Length / df$Sepal.Width
df$Petal.Ratio <- df$Petal.Length / df$Petal.Width
head(df, 3)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species Sepal.Ratio
1          5.1         3.5          1.4         0.2  setosa    1.457143
2          4.9         3.0          1.4         0.2  setosa    1.633333
3          4.7         3.2          1.3         0.2  setosa    1.468750
  Petal.Ratio
1         7.0
2         7.0
3         6.5

df.ratio <- df[, c('Species', 'Sepal.Ratio', 'Petal.Ratio')]
head(df.ratio, 3)

  Species Sepal.Ratio Petal.Ratio
1  setosa    1.457143         7.0
2  setosa    1.633333         7.0
3  setosa    1.468750         6.5

df$Sepal.Ratio <- NULL
df$Petal.Ratio <- NULL
head(df, 3)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa

Crear dataframe

df.ratio <- data.frame(
                Species = df$Species,
                Sepal.Ratio = df$Sepal.Length / df$Sepal.Width,
                Petal.Ratio = df$Petal.Length / df$Petal.Width
            )
head(df.ratio)

  Species Sepal.Ratio Petal.Ratio
1  setosa    1.457143        7.00
2  setosa    1.633333        7.00
3  setosa    1.468750        6.50
4  setosa    1.483871        7.50
5  setosa    1.388889        7.00
6  setosa    1.384615        4.25

Función aggregate

La función aggregate() es muy util para calcular estadisticos por subconjuntos del data frame.

aggregate(df[, c(1:4)], by = list(Species = df$Species), FUN = mean)

     Species Sepal.Length Sepal.Width Petal.Length Petal.Width
1     setosa        5.006       3.428        1.462       0.246
2 versicolor        5.936       2.770        4.260       1.326
3  virginica        6.588       2.974        5.552       2.026

aggregate(df[, c(1:4)], by = list(Species = df$Species), FUN = sd)

     Species Sepal.Length Sepal.Width Petal.Length Petal.Width
1     setosa    0.3524897   0.3790644    0.1736640   0.1053856
2 versicolor    0.5161711   0.3137983    0.4699110   0.1977527
3  virginica    0.6358796   0.3224966    0.5518947   0.2746501

Drosophila melanogaster

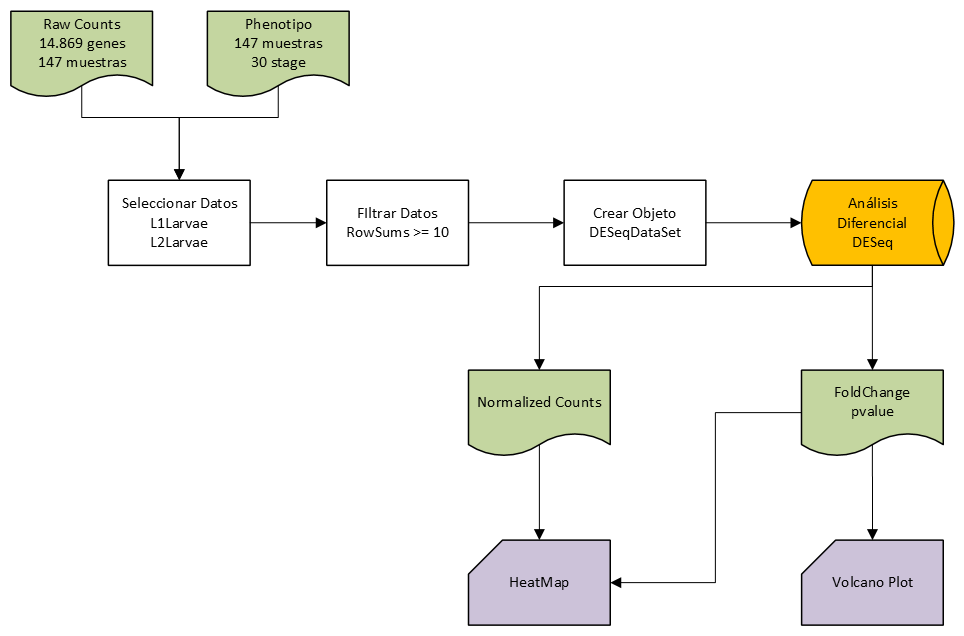
Para el análisis de expresión diferencial vamos a utilizar el paquete DESeq2.

Debemos familiarizarnos con la función a usar:

La función DESeq() recibe como paramatro un objeto de la clase DESeqDataSet. Este tipo de variable almacena los valores de entrada, calculos intermedios y resultados del análisis.

dds <- DeSeqDataSetFromMatrix(countData, colData, design)

countData: Es una matriz númerica (muestras en columnas).
colData: DataFrame con al menos una columna, las filas corresponden a las columnas del countData.
design: Expresa como las cuentas para cada gen dependen de las variables en colData.

Drosophila Melanogaster

Raw counts

df <- read.csv('data/mcf_count_table.csv')

dim(df)

[1] 14869   148

head(df)

         gene SRX007811 SRX008180 SRX008227 SRX008238 SRX008258 SRX008015
1 FBgn0000003         0         0         0         0         0         0
2 FBgn0000008      3903      1601       681       648       718       921
3 FBgn0000014        75        29        10         9        12       563
4 FBgn0000015        33        11         8         4         8       235
5 FBgn0000017      9763      4107      1814      1652      1788      6358
6 FBgn0000018       832       368       146       126       170        97
  SRX008179 SRX008190 SRX008193 SRX008271 SRX008027 SRX008181 SRX008217
1         0         0         0         0         0         0         0
2       295       364       268       267      1764       411       284
3       186       239       152       191      4890       957       806
4        95       101        58       101      3000       590       492
5      2214      2763      1906      2053      6006      1252       904
6        33        55        25        22       339        57        60
  SRX008250 SRX008265 SRX008025 SRX008175 SRX008210 SRX008212 SRX008257
1         0         0         0         0         0         0         0
2       396       706      1074       563       156       160       440
3      1036      1956      6147      3166       956      1053      2876
4       715      1185      2492      1228       340       458      1174
5      1244      2456      5030      2584       746       847      2105
6        71       116       178        95        34        35        75
  SRX008010 SRX008249 SRX008252 SRX008273 SRX008274 SRX008005 SRX008198
1         0         0         0         0         0         0         0
2      1557       874       904       632       234      4488      1222
3      5160      3270      2836      2048       815      4792      1390
4      1986      1454      1138       788       324      1709       541
5      5350      3101      3046      2343       969      8695      2448
6       130        99        75        56        25       141        43
  SRX008208 SRX008243 SRX008247 SRX008018 SRX008177 SRX008225 SRX008235
1         0         0         0         0         0         0         0
2       825      3030      1224      8755      2431      1718      5478
3       883      3102      1192      9943      2536      1890      5782
4       370      1076       431      3421       886       744      1942
5      1518      5540      2345     12295      3296      2440      7652
6        25        97        34       229        59        50       113
  SRX008277 SRX008007 SRX008196 SRX008233 SRX008237 SRX008262 SRX008006
1         0         0         0         0         0         0         0
2      2212      5617      1039      2769      1716      1664      1749
3      2559      5134       935      2339      1404      1426      2908
4       985      1313       240       645       392       419      1024
5      3125      9374      1816      4564      2640      2853      4548
6        48       122        19        67        27        44        93
  SRX008178 SRX008205 SRX008242 SRX008278 SRX008020 SRX008213 SRX008215
1         0         0         0         0         0         0         0
2      1532       549       715       390      1685       384      1397
3      2602       965      1116       638      2333       543      1832
4       845       321       398       216       914       199       667
5      4156      1537      1816      1085      2577       572      2010
6        57        20        23        10        42        18        31
  SRX008222 SRX008259 SRX008011 SRX008214 SRX008221 SRX008241 SRX008256
1         0         0         0         0         0         0         0
2       407      2141      1036       417       353       560       394
3       512      3101      1068       448       338       589       475
4       217      1153       419       165       139       219       179
5       526      3328      3327      1425      1046      1719      1342
6        12        72        35        16        11        15        15
  SRX008019 SRX008167 SRX008234 SRX008251 SRX008266 SRX008026 SRX008174
1         0         0         0         0         0         0         0
2      2548       730       687       786       587       928       392
3      3090       979       819      1008       810      1845       796
4      1306       404       334       450       310       635       295
5      6979      1985      1843      2297      1539      1440       670
6       113        33        26        39        23       150        64
  SRX008201 SRX008239 SRX008008 SRX008168 SRX008211 SRX008255 SRX008261
1         0         0         0         0         0         0         0
2       575       851      1696       353       284       733       258
3      1203      1740      2030       422       375       914       296
4       485       617       695       155       130       350        95
5      1021      1330      2360       481       434      1054       381
6       102       139       371        94        66       162        49
  SRX008009 SRX008194 SRX008207 SRX008224 SRX008244 SRX008029 SRX008184
1         0         0         0         0         0         0         0
2       311        94       108       110       148       228        74
3       536       182       211       196       296       535       181
4       190        71        70        81       111       127        56
5       481       154       197       197       292       667       226
6        83        29        27        35        48       131        63
  SRX008206 SRX008220 SRX008267 SRX008014 SRX008182 SRX008187 SRX008189
1         0         0         0         0         0         0         0
2       115        77        74       393       541       168       161
3       278       212       173       822      1342       360       434
4        62        56        44       166       324        82        95
5       357       242       216      1036      1416       490       452
6        82        48        57       107       167        44        57
  SRX008200 SRX008156 SRX008199 SRX008245 SRX008253 SRX008023 SRX008218
1         0         0         0         0         0         0         0
2       163      1205      2939       945      1022      3602       926
3       398      1598      3795      1136      1349      3227       836
4       103       389      1029       322       338       470       134
5       423      1791      4400      1395      1484      5073      1312
6        39       154       334        94       124       307        78
  SRX008246 SRX008248 SRX008275 SRX008016 SRX008192 SRX008219 SRX008236
1         0         0         0         0         0         0         0
2      2209      1494      1076      4011      1233      1758      2123
3      1903      1231       878      2698       885      1115      1577
4       287       201       130       529       192       229       325
5      3019      1972      1521      5793      1860      2517      3176
6       178       105        80       274        95       128       156
  SRX008264 SRX008013 SRX008188 SRX008197 SRX008228 SRX008022 SRX008183
1         0         0         0         0         0         0         0
2      2023      1117      1004      1447      1452       665       396
3      1488       282       286       355       379        61        44
4       316        99        87       153       101        17        19
5      2960      2356      2159      3069      3182      2170      1317
6       148       264       247       320       333       218       149
  SRX008185 SRX008216 SRX012269 SRX008024 SRX008173 SRX008195 SRX008202
1         0         0         0         0         0         0         0
2       686       409      1011       603       336       380       431
3        64        36        72        39        35        40        36
4        17        15        20        15        17        20         8
5      2252      1426      3357      1906      1123      1239      1551
6       220       137       343       194       138       164       143
  SRX008254 SRX012270 SRX008012 SRX008170 SRX008263 SRX008268 SRX016332
1         0         0         0         0         0         0         0
2       437       738       717       630       389       303       373
3        29        54       340       307       195       148       222
4        10        12       256       270       165       116       142
5      1410      2504      1388      1279       790       579       849
6       136       224       170       186       107        76       108
  SRX008028 SRX008191 SRX008223 SRX008260 SRX008021 SRX008203 SRX008226
1         0         0         0         0         0         0         0
2      1234      1112       989      1026       430       200       158
3       309       298       243       281       137        75        47
4       347       292       305       328       167       118        70
5      2007      1837      1596      1644       898       461       341
6       319       280       251       308       154        98        54
  SRX008229 SRX008232 SRX012271 SRX008171 SRX008186 SRX008240 SRX010758
1         0         0         0         0         0         0         0
2       430       250      1074      3386      6313      3210      4811
3       132        74       339       647      1310       632       939
4       177        98       322       202       375       203       259
5       777       504      2100      2759      5211      2524      3931
6       137        71       332       128       263        96       165
  SRX016331 SRX008155 SRX008169 SRX008172 SRX008231 SRX008542 SRX008017
1         0         0         0         0         0         0         0
2      3803      2393      1834      1890       744       952       971
3       751       572       404       440       156       212       307
4       219       252       183       210        76        81       146
5      3212      2584      2013      2156       809       963      1168
6       117       216       142       143        47        65       134
  SRX008209 SRX008230 SRX008270 SRX008157 SRX008204 SRX008269 SRX008272
1         0         0         0         0         0         0         0
2       844      1204       620      1519      1267      1448      1185
3       253       371       159      1841      1650      1875      1370
4       146       168        93       340       332       368       261
5      1085      1513       782      1973      1592      1833      1465
6       124       146        82       101       112       116       102
  SRX008276
1         0
2      3225
3      4048
4       711
5      4066
6       294

Metadatos

metadata <- read.csv('data/mcf_metadata.csv')
dim(metadata)

[1] 147   3

head(metadata, 20)

   sample.id num.tech.reps       stage
1  SRX007811             5 Embryos0002
2  SRX008180             2 Embryos0002
3  SRX008227             1 Embryos0002
4  SRX008238             1 Embryos0002
5  SRX008258             1 Embryos0002
6  SRX008015             2 Embryos0204
7  SRX008179             1 Embryos0204
8  SRX008190             1 Embryos0204
9  SRX008193             1 Embryos0204
10 SRX008271             1 Embryos0204
11 SRX008027             4 Embryos0406
12 SRX008181             1 Embryos0406
13 SRX008217             1 Embryos0406
14 SRX008250             1 Embryos0406
15 SRX008265             2 Embryos0406
16 SRX008025             5 Embryos0608
17 SRX008175             2 Embryos0608
18 SRX008210             1 Embryos0608
19 SRX008212             1 Embryos0608
20 SRX008257             2 Embryos0608

Fenotipos seleccionados

Queremos seleccionar las muestras que corresponden con el stage ‘L1Larvae’ y ‘L2Larvae’.

fenotipos <- c('L1Larvae', 'L2Larvae')

df.fenotipos <- metadata[metadata$stage %in% fenotipos, c('sample.id', 'stage')]

df.fenotipos$stage <- as.factor(df.fenotipos$stage)

df.fenotipos

   sample.id    stage
61 SRX008026 L1Larvae
62 SRX008174 L1Larvae
63 SRX008201 L1Larvae
64 SRX008239 L1Larvae
65 SRX008008 L2Larvae
66 SRX008168 L2Larvae
67 SRX008211 L2Larvae
68 SRX008255 L2Larvae
69 SRX008261 L2Larvae

Filtrar el dataset por las muestras seleccionadas

head(names(df), 15)

 [1] "gene"      "SRX007811" "SRX008180" "SRX008227" "SRX008238" "SRX008258"
 [7] "SRX008015" "SRX008179" "SRX008190" "SRX008193" "SRX008271" "SRX008027"
[13] "SRX008181" "SRX008217" "SRX008250"

df.sub <- df[, df.fenotipos$sample.id]

head(df.sub)

  SRX008026 SRX008174 SRX008201 SRX008239 SRX008008 SRX008168 SRX008211
1         0         0         0         0         0         0         0
2       928       392       575       851      1696       353       284
3      1845       796      1203      1740      2030       422       375
4       635       295       485       617       695       155       130
5      1440       670      1021      1330      2360       481       434
6       150        64       102       139       371        94        66
  SRX008255 SRX008261
1         0         0
2       733       258
3       914       296
4       350        95
5      1054       381
6       162        49

Añadir genes

rownames(df.sub) <- df$gene

head(df.sub)

            SRX008026 SRX008174 SRX008201 SRX008239 SRX008008 SRX008168
FBgn0000003         0         0         0         0         0         0
FBgn0000008       928       392       575       851      1696       353
FBgn0000014      1845       796      1203      1740      2030       422
FBgn0000015       635       295       485       617       695       155
FBgn0000017      1440       670      1021      1330      2360       481
FBgn0000018       150        64       102       139       371        94
            SRX008211 SRX008255 SRX008261
FBgn0000003         0         0         0
FBgn0000008       284       733       258
FBgn0000014       375       914       296
FBgn0000015       130       350        95
FBgn0000017       434      1054       381
FBgn0000018        66       162        49

TIP

fenotipos <- c('L1Larvae', 'L2Larvae')
df.fenotipos <- metadata[metadata$stage %in% fenotipos, c('sample.id', 'stage')]

df.sub <- df[, df.fenotipos$sample.id]
rownames(df.sub) <- df$gene

¿No es más sencillo?

df.sub <- df[, c('SRX008026', 'SRX008174 ', 'SRX008201', 'SRX008239', 'SRX008008 ', 
                 ' SRX008168', 'SRX008211', 'SRX008255', 'SRX008261')]
rownames(df.sub) <- df$gene

Eliminar genes con pocas counts

head(rowSums(df.sub))

FBgn0000003 FBgn0000008 FBgn0000014 FBgn0000015 FBgn0000017 FBgn0000018 
          0        6070        9621        3457        9171        1197

keep <- rowSums(df.sub) >= 10
head(keep)

FBgn0000003 FBgn0000008 FBgn0000014 FBgn0000015 FBgn0000017 FBgn0000018 
      FALSE        TRUE        TRUE        TRUE        TRUE        TRUE

df.sub  <- df.sub [keep, ]
head(df.sub)

            SRX008026 SRX008174 SRX008201 SRX008239 SRX008008 SRX008168
FBgn0000008       928       392       575       851      1696       353
FBgn0000014      1845       796      1203      1740      2030       422
FBgn0000015       635       295       485       617       695       155
FBgn0000017      1440       670      1021      1330      2360       481
FBgn0000018       150        64       102       139       371        94
FBgn0000024      1797       707      1126      1498      1701       341
            SRX008211 SRX008255 SRX008261
FBgn0000008       284       733       258
FBgn0000014       375       914       296
FBgn0000015       130       350        95
FBgn0000017       434      1054       381
FBgn0000018        66       162        49
FBgn0000024       334       791       235

dim(df.sub)

[1] 11342     9

DESeq2

Para el análisis de expresión diferencial vamos a utilizar el paquete DESeq2.

Vignettes: Analyzing RNA-seq data with DESeq2

install.packages("BiocManager")

BiocManager::install("DESeq2")

DESeq2

library(DESeq2)
coldata <- data.frame(stage = df.fenotipos$stage)
rownames(coldata) <- df.fenotipos$sample.id
head(coldata)

             stage
SRX008026 L1Larvae
SRX008174 L1Larvae
SRX008201 L1Larvae
SRX008239 L1Larvae
SRX008008 L2Larvae
SRX008168 L2Larvae

dds <- DESeqDataSetFromMatrix(
                    countData = df.sub,
                    colData = coldata,
                    design = ~stage
            )

dds

class: DESeqDataSet 
dim: 11342 9 
metadata(1): version
assays(1): counts
rownames(11342): FBgn0000008 FBgn0000014 ... FBgn0261574 FBgn0261575
rowData names(0):
colnames(9): SRX008026 SRX008174 ... SRX008255 SRX008261
colData names(1): stage

DESeq2

dds <- DESeq(dds)
dds

class: DESeqDataSet 
dim: 11342 9 
metadata(1): version
assays(4): counts mu H cooks
rownames(11342): FBgn0000008 FBgn0000014 ... FBgn0261574 FBgn0261575
rowData names(22): baseMean baseVar ... deviance maxCooks
colnames(9): SRX008026 SRX008174 ... SRX008255 SRX008261
colData names(2): stage sizeFactor

res <- results(dds, contrast = c('stage', 'L1Larvae', 'L2Larvae'))
res

log2 fold change (MLE): stage L1Larvae vs L2Larvae 
Wald test p-value: stage L1Larvae vs L2Larvae 
DataFrame with 11342 rows and 6 columns
             baseMean log2FoldChange     lfcSE      stat      pvalue
            <numeric>      <numeric> <numeric> <numeric>   <numeric>
FBgn0000008   562.467      0.0567848 0.0548497   1.03528 3.00538e-01
FBgn0000014   894.891      0.7973618 0.0453627  17.57748 3.66521e-69
FBgn0000015   323.316      0.8453126 0.0737835  11.45666 2.17741e-30
FBgn0000017   862.122      0.2538049 0.0478014   5.30957 1.09886e-07
FBgn0000018   111.781     -0.3815511 0.1121942  -3.40081 6.71867e-04
...               ...            ...       ...       ...         ...
FBgn0261570 1415.4046       0.215624 0.0667683   3.22944 1.24034e-03
FBgn0261572   71.9698       2.201588 0.1526436  14.42307 3.70504e-47
FBgn0261573  311.1002       0.311384 0.0678953   4.58624 4.51307e-06
FBgn0261574 1477.7729       0.557713 0.0445722  12.51255 6.37406e-36
FBgn0261575 1214.1409      -0.346767 0.0481108  -7.20769 5.69101e-13
                   padj
              <numeric>
FBgn0000008 3.49975e-01
FBgn0000014 2.56904e-68
FBgn0000015 8.69814e-30
FBgn0000017 2.25929e-07
FBgn0000018 1.08511e-03
...                 ...
FBgn0261570 1.95915e-03
FBgn0261572 1.96258e-46
FBgn0261573 8.46415e-06
FBgn0261574 2.79645e-35
FBgn0261575 1.45364e-12

Guardar resultados

Guardamos los resultados del análisis diferencial y los datos normalizados

write.csv(res, 'data/DGE.csv')

write.csv(counts(dds, normalized=TRUE), 'data/normalized_counts.csv')

Volver